Skip to content

ELO Rating System

In adversarial games, the cumulative environment reward may not be a meaningful metric by which to track learning progress.

This is because the cumulative reward is entirely dependent on the skill of the opponent.

An agent at a particular skill level will get more or less reward against a worse or better agent, respectively.

Instead, it's better to use ELO rating system, a method to calculate the relative skill level between two players in a zero-sum game.

If the training performs correctly, this value should steadily increase.

What is a zero-sum game?

A zero-sum game is a game where each player's gain or loss of utility is exactly balanced by the gain or loss of the utility of the opponent.

Simply explained, we face a zero-sum game when one agent gets +1.0, its opponent gets -1.0 reward.

For instance, Tennis is a zero-sum game: if you win the point you get +1.0 and your opponent gets -1.0 reward.

How works the ELO Rating System

  • Each player has an initial ELO score. It's defined in the initial_elo trainer config hyperparameter.

  • The difference in rating between the two players serves as the predictor of the outcomes of a match.

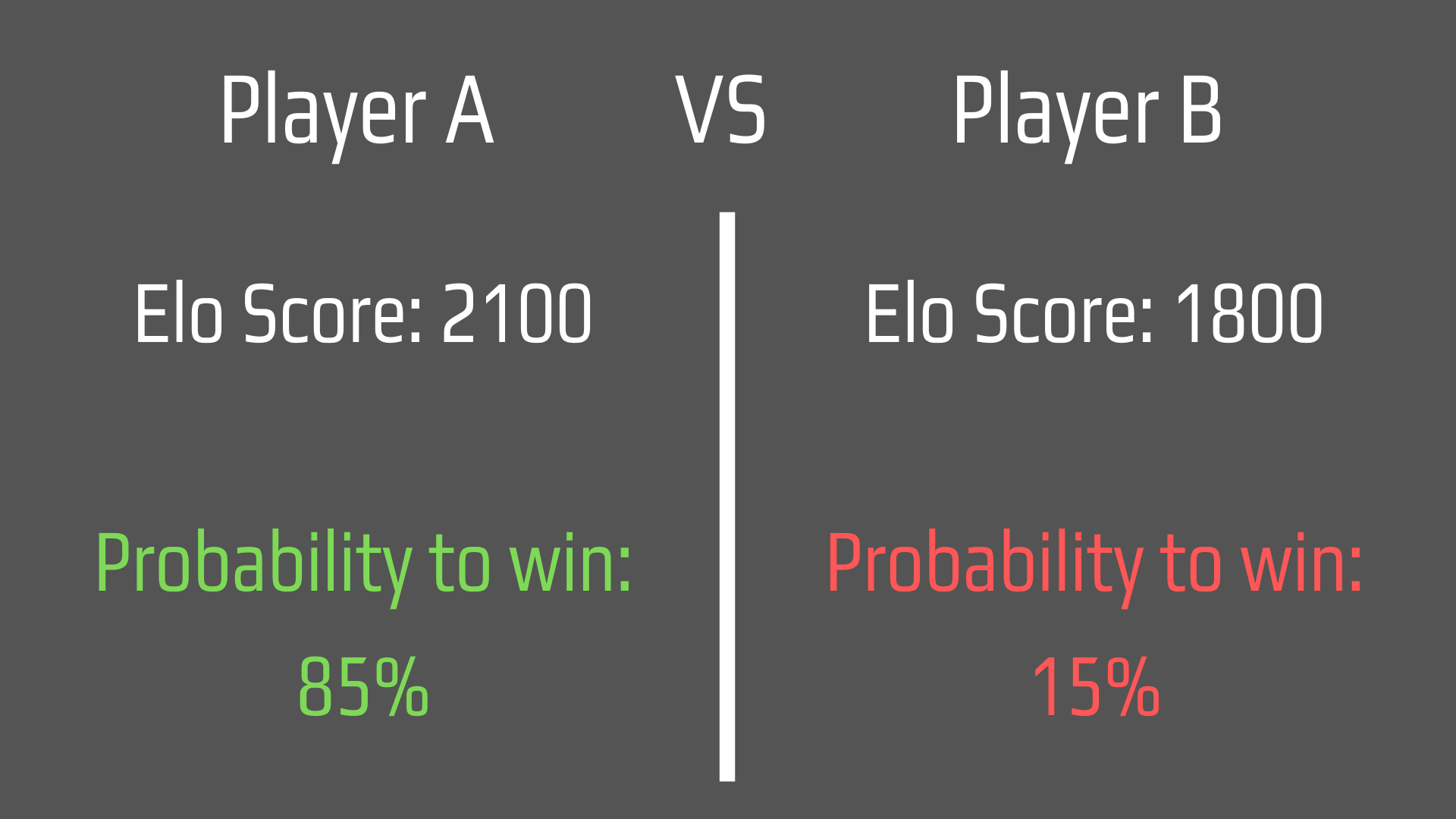Example Elo For instance, if player A has an Elo score of 2100 and player B has an ELO score of 1800 the chance that player A wins is 85% against 15% for player b.

  • We calculate the expected score of each player using this formula:

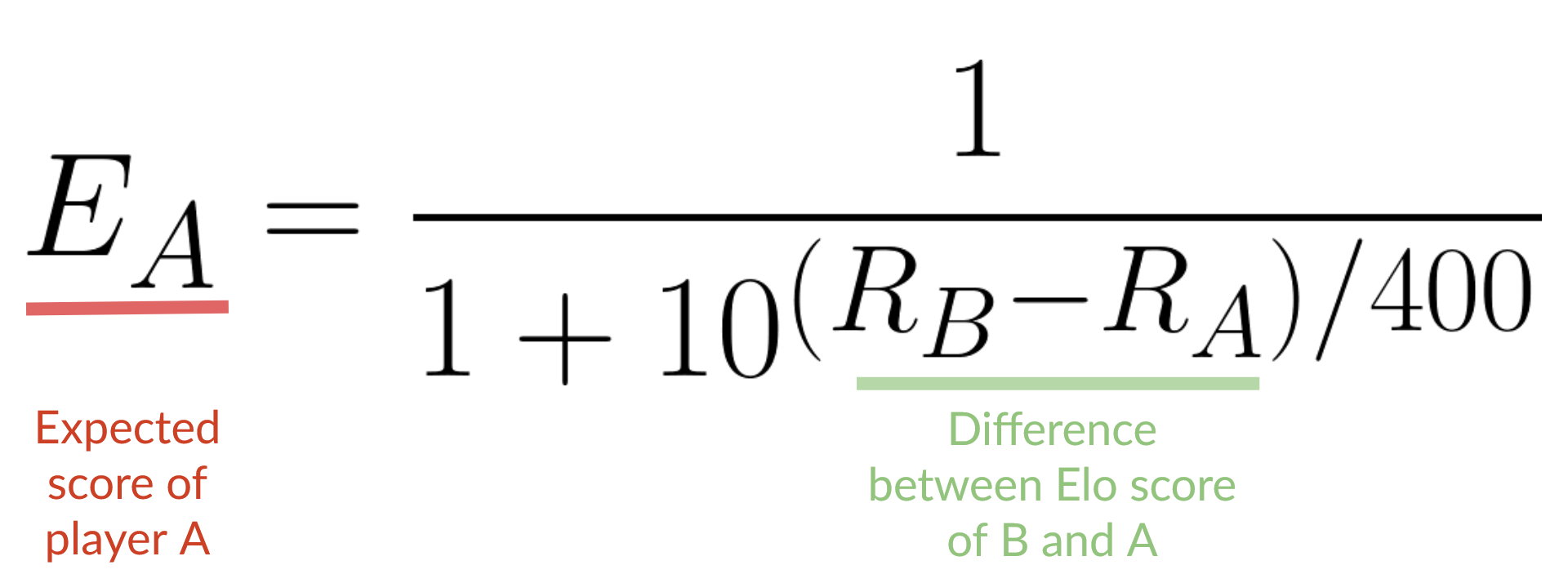
Elo Expected Score Formula

  • At the end of the game, based on the outcome we update the player’s actual Elo score, we use a linear adjustment proportional to the amount by which the player over-performed or under-performed. The winning player takes points from the losing one:
  • If the higher-rated player wins → a few points will be taken from the lower-rated player.
  • If the lower-rated player wins → a lot of points will be taken from the high-rated player.

  • If it’s a draw → the lower-rated player gains a few points from higher.

  • We update players rating using this formula:

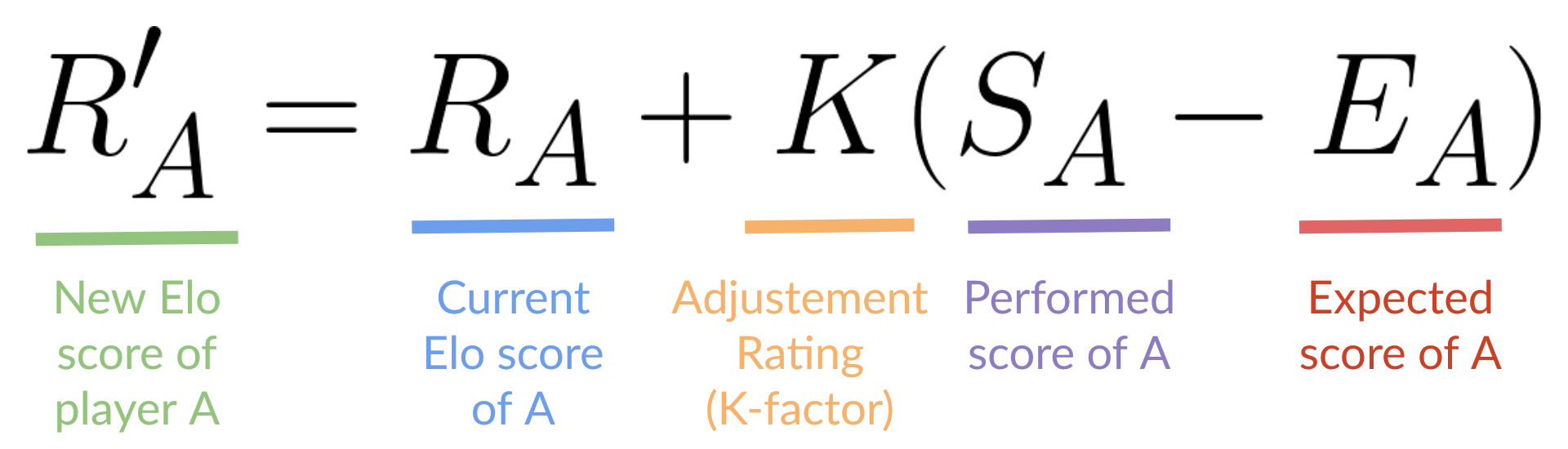
Elo Score Update Formula

The Tennis example

  • We start to train our agents.
  • Both of them have the same skills. So ELO score for each of them that we defined using parameter initial_elo = 1200.0.

We calculate the expected score E: Ea = 0.5 Eb = 0.5

So it means that each player has 50% chances of winning the point.

If A wins, the new rating R would be:

Ra = 1200 + 16 * (1 - 0.5) → 1208

Rb = 1200 + 16 * (0 - 0.5) → 1192

Player A has now an ELO score of 1208 and Player B an ELO score of 1192. Therefore, Player A is now a little bit better than Player B.